Subset-Sum Problem

Given a bag of elements, find all the subsets of the elements that sum to a given target.

For example:

>>> subset_sum(bag=[3, 2, 2, 1, 1, 1, 1], target=7)
[
  (3, 2, 2),
  (3, 2, 1, 1),
  (2, 2, 1, 1, 1),
  (3, 1, 1, 1, 1),
]

Assumptions

• The integers are strictly non-negative
• We do not want duplicate subsets
• The input lists are sorted

Algorithm

The following algorithm using dynamic programming (courtesy of GitHub Copilot):

def subset_sum(numbers, target):
    bins = [set() for _ in range(target + 1)]
    bins[0].add(())
    for num in numbers:
        for t in range(target, num - 1, -1):
            for prev in bins[t - num]:
                bins[t].add(prev + (num,))
    return bins[target]

Complexity

Runtime: $O(n_{bag}\times target)$
Space: $O(n_{bag}\times target)$

Intuition

• We create “bins” for (0..target), where each bin contains the combination of elements that sum to that given bin’s number
• For a given element, we want to memoize the result by adding that element to the subset of elements element steps away. Below is an example for an element 2, acting on bin 6:
  
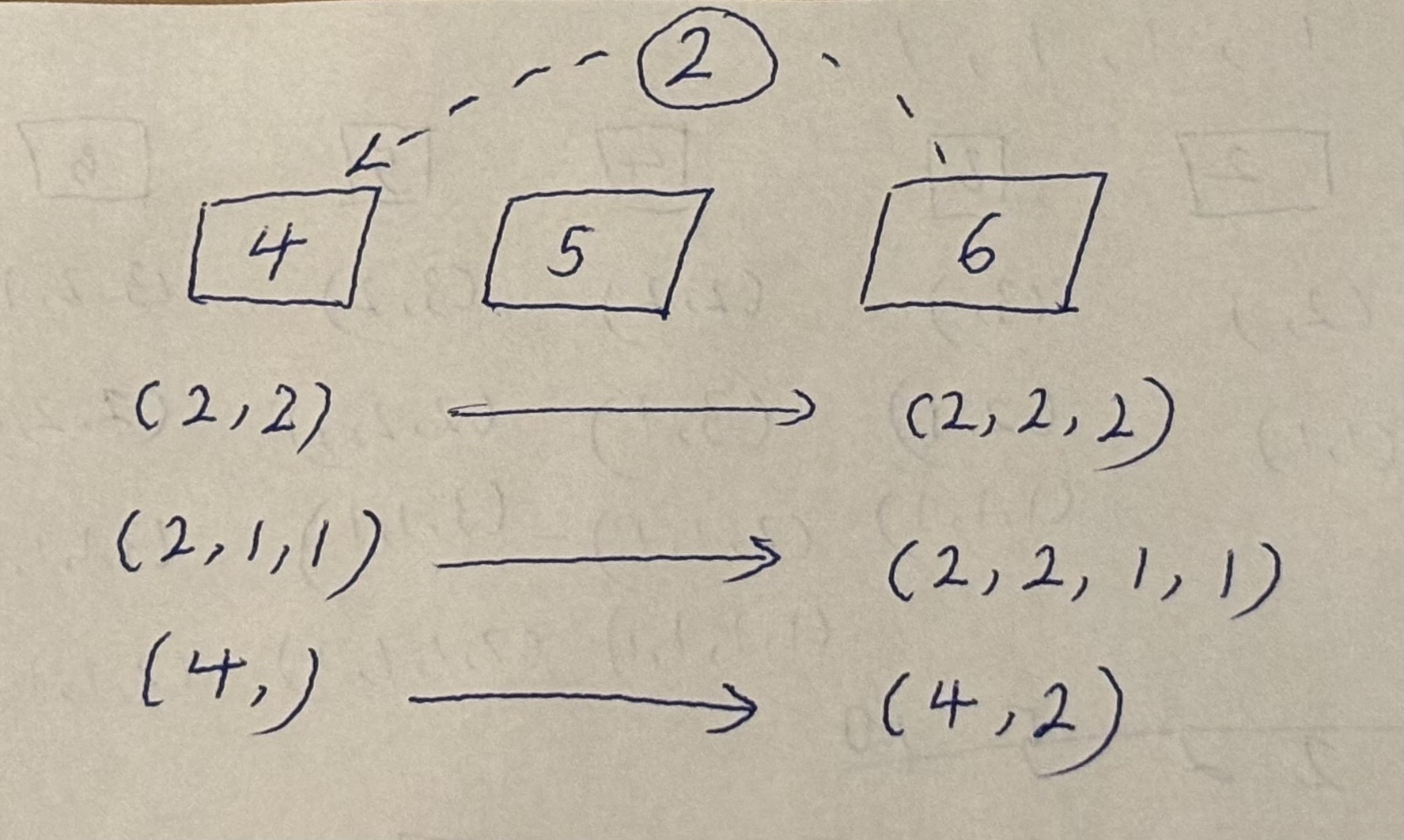
• The beauty is that if there are duplicates, the operation above doesn’t change anything, since bins[i]: set[tuple[int]].
  • Because tuple[int] is used, it means that the input list has to be sorted. Otherwise, you’ll get tuple[int]s that are merely permutations of the same subset of elements (e.g. (2, 1, 3) and (3, 1, 2)). There are two ways to account for it:
    • Sort the input (simplest!)
    • Use a Counter data structure
  • Yet another beauty is that the solution still works even if you swap the ordering of the bag of elements
• When performing the operation above, it has to be done backwards, as shown by the range(target, num - 1, -1). This is because we are using the result of bins[t - num] for bins[t]. Had we operated non-reversed, we would have double/triple/multiple-counted a given element (num)‘s contribution to a set.